Why Does 45º Launch Angle Give Maximum Range? // HSC Physics
TLDRThe video script delves into the principles of projectile motion, highlighting the critical role of launch angle in achieving maximum range. It explains that an angle of 45 degrees results in the longest range due to the interplay between the object's initial vertical and horizontal velocity components. The script further clarifies this concept through mathematical expressions, demonstrating that the range is maximized when the launch angle allows for the optimal combination of these velocity components, which occurs at 45 degrees, given a constant initial velocity and gravitational acceleration.
Takeaways
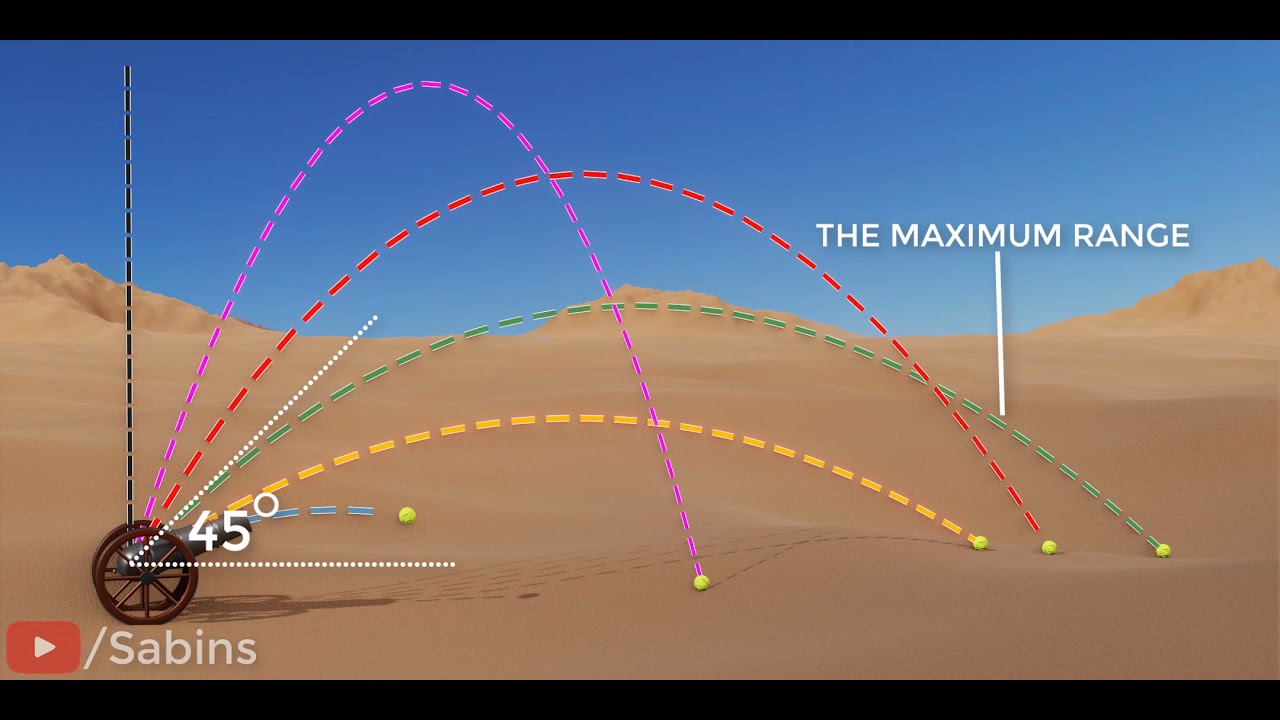
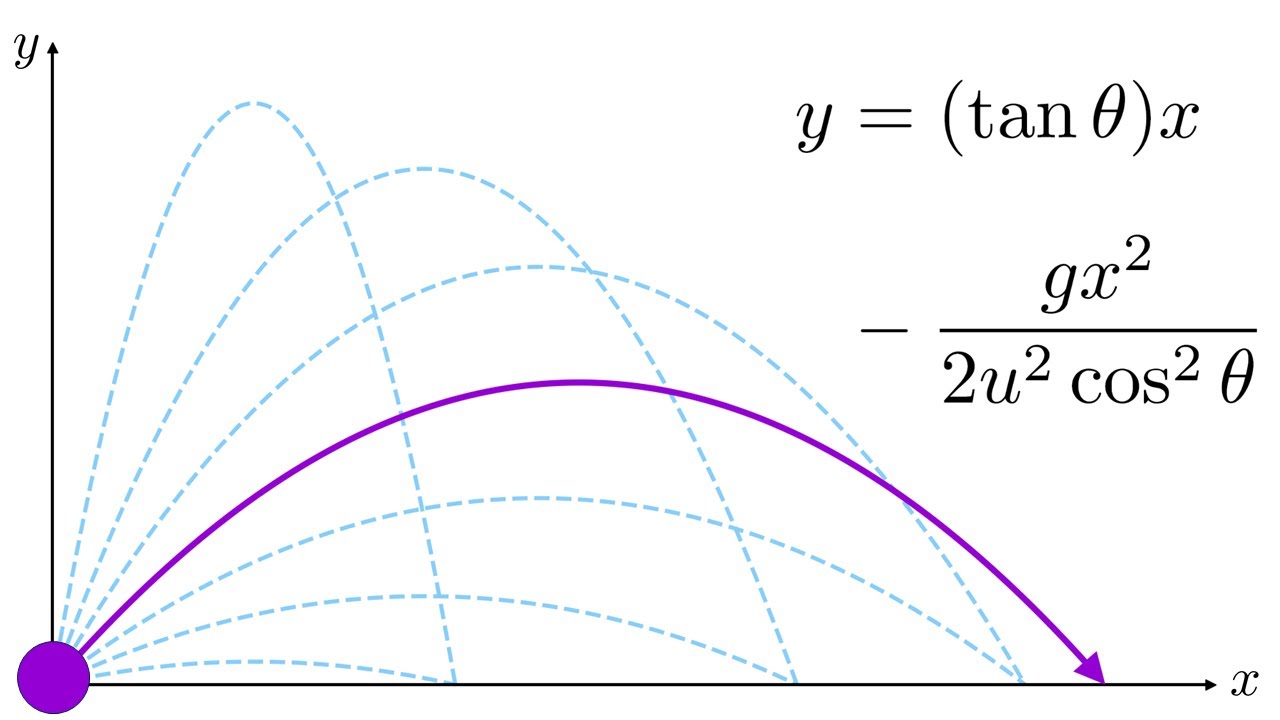
- 💡 The maximum range of a projectile, given an initial velocity, is achieved at a launch angle of 45 degrees.
- 💡 Below or above a 45-degree angle, the range of a projectile decreases from its maximum value.
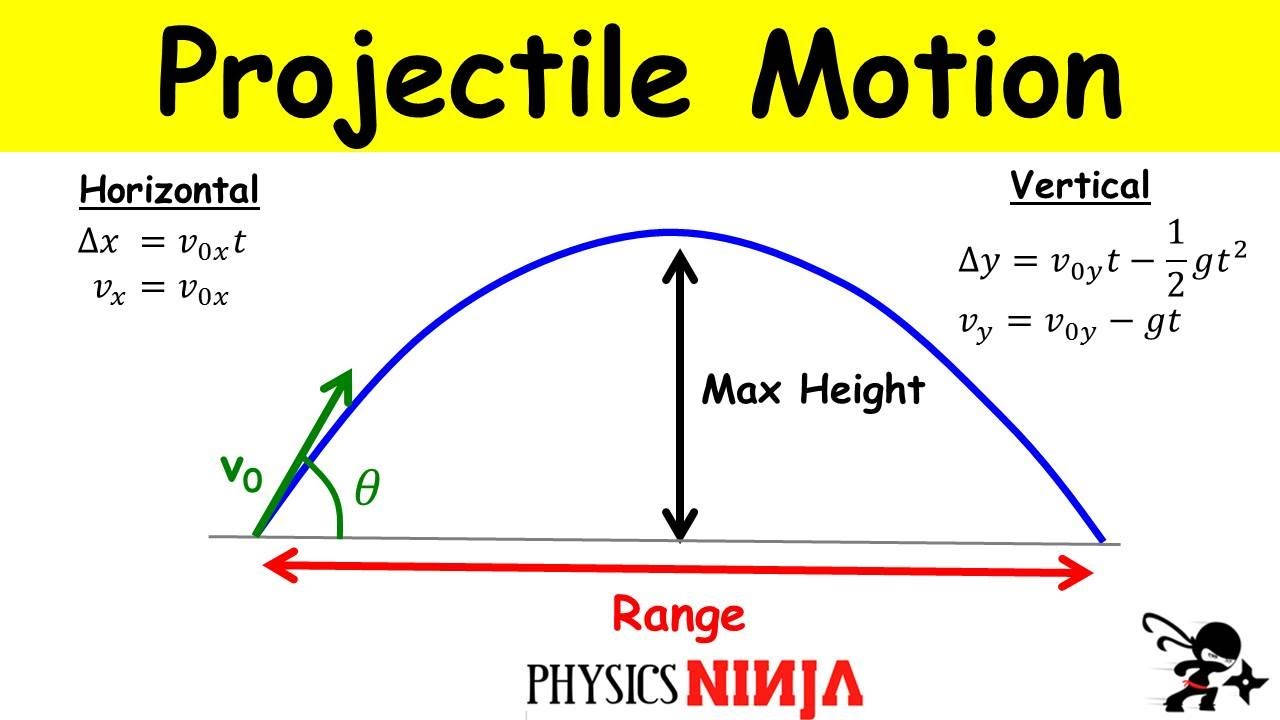
- 💡 The range of a projectile in the absence of air resistance is the product of its initial horizontal velocity and time of flight.
- 💡 Time of flight can be calculated using the vertical displacement equation, which depends on the initial vertical velocity.
- 💡 A larger initial vertical velocity results in a longer time of flight, affecting the projectile's range.
- 💡 The projectile's range depends on both its initial horizontal and vertical velocities.
- 💡 For a projectile returning to its launch height, the vertical displacement at the end is zero.
- 💡 Time of flight equations can be derived from initial velocity components and gravity, showing the dependency on launch angle.
- 💡 Trigonometry, specifically the double angle formula, is used to simplify the expression for the projectile's range.
- 💡 The maximum range occurs when the launch angle allows the sine of double the angle to equal 1, which corresponds to a 45-degree launch angle.
Q & A
Why is 45 degrees considered the optimal launch angle for maximum range in projectile motion?
-45 degrees is considered the optimal launch angle for maximum range because at this angle, the sine of double the angle (sine 2θ) reaches its maximum value of 1. This results from the trigonometric identity that sine 2θ equals 2 sine θ times cosine θ, maximizing the range for given initial velocity and gravitational acceleration.
How does changing the launch angle from 45 degrees affect the range of a projectile?
-Changing the launch angle from 45 degrees in either direction (increasing or decreasing) results in a decrease from the maximum range. This is because the sine of double the angle, which directly affects the range, is maximized at 45 degrees or when 2θ equals 90 degrees.
What role does the initial vertical velocity play in determining the range of a projectile?
-The initial vertical velocity directly affects the time of flight of a projectile. A higher initial vertical velocity results in a longer time of flight, and since range is the product of horizontal velocity and time of flight, the initial vertical velocity influences the range.
How is the time of flight of a projectile calculated in the absence of air resistance?
-The time of flight can be derived using the equation of vertical motion, Sy = uy*t + 0.5*g*t^2, where Sy is the vertical displacement, uy is the initial vertical velocity, g is the gravitational acceleration, and t is the time. By setting Sy to zero for a projectile returning to its launch height, we can solve for the time of flight.
What is the significance of the gravitational acceleration (g) in the equations of projectile motion?
-Gravitational acceleration (g) is significant as it represents the constant acceleration downwards due to gravity, affecting both the vertical displacement and the time of flight of the projectile. It is inversely proportional to the range in the final equation, indicating that gravity plays a pivotal role in the motion of a projectile.
Can the range of a projectile be affected by factors other than the launch angle and initial velocity?
-In the theoretical model discussed, the range is primarily affected by the launch angle, initial velocity, and gravitational acceleration. However, in real-world scenarios, other factors like air resistance, altitude, and wind can significantly affect the projectile's range.
Why does the range formula involve sine and cosine functions of the launch angle?
-The range formula involves sine and cosine functions of the launch angle because these trigonometric functions determine the vertical and horizontal components of the initial velocity. The interplay between these components through the sine 2θ identity directly influences the range of the projectile.
What does the equation R = (U^2 * sin(2θ)) / g tell us about the relationship between range and launch angle?
-This equation shows that the range (R) of a projectile is directly proportional to the square of its initial velocity (U^2) and the sine of twice the launch angle (sin(2θ)), and inversely proportional to gravitational acceleration (g). This indicates that the range is maximized when sin(2θ) is at its peak, which occurs at a launch angle of 45 degrees.
How does the concept of vertical displacement (Sy) relate to the time of flight in projectile motion?
-The concept of vertical displacement (Sy) is crucial in calculating the time of flight, especially when considering a projectile that lands back at its initial height (Sy = 0). This condition allows for solving the time of flight in terms of the initial vertical velocity and gravitational acceleration.
What is the significance of the trigonometric identity involving sine 2θ in the context of projectile motion?
-The significance of the sine 2θ trigonometric identity in projectile motion lies in its ability to simplify the range equation into a form that clearly shows the dependency of range on the launch angle. By representing the product of sine and cosine of the launch angle as sine 2θ, it reveals how the range reaches its maximum at a 45-degree launch angle.
Outlines
📐 Projectile Motion and Maximum Range
This paragraph discusses the principles of projectile motion, focusing on how a 45-degree launch angle achieves maximum range for an object given a specific initial velocity. It explains the relationship between launch angle and range using a graph and delves into the mathematical expressions that govern range in the absence of air resistance. The explanation includes the equations for range, time of flight, and the components of initial velocity, ultimately showing that the maximum range is achieved when the launch angle allows for the greatest product of horizontal velocity and time of flight. The importance of trigonometry in understanding these principles is highlighted, with a focus on the double angle formula for sine and its application in determining the optimal launch angle for maximum range.
Mindmap
Keywords
💡Projectile Motion
💡Initial Velocity
💡Launch Angle
💡Range
💡Horizontal Component Velocity
💡Vertical Component Velocity
💡Time of Flight
💡Gravitational Acceleration
💡Air Resistance
💡Trigonometry
Highlights
Maximum range of a projectile is achieved at a 45-degree launch angle.
Range decreases from its maximum when the launch angle is less than or greater than 45 degrees.
Range of an object in projectile motion is given by initial horizontal velocity multiplied by time of flight.
Time of flight depends on the initial vertical velocity.
A larger initial vertical velocity results in a longer time of flight.
The range is affected by both horizontal and vertical components of initial velocity.
For objects that land at the same vertical position they were launched from, the vertical displacement at the end of motion is zero.
Time of flight can be derived using the equation of vertical displacement.
The initial vertical component is a function of initial velocity and sine of launch angle.
The range formula involves initial velocity, launch angle, and gravitational acceleration.
A trigonometry double angle formula shows sine of twice the launch angle equals 2 times sine of launch angle times cosine of launch angle.
Maximum range occurs when sine of twice the launch angle equals 1.
Sine of 90 degrees gives the maximum value of 1, indicating maximum range at a 45-degree launch angle.
The range of a projectile is inversely proportional to gravitational acceleration.
For a given initial velocity and gravitational acceleration, the launch angle of 45 degrees yields maximum range.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: